使用递归回溯算法实现的前端解数独游戏

前言

最近一个多月来，我一直全身心投入于数据结构和算法的学习，一边学习各种典型的算法类型，一边疯狂刷题，从一个对算法一无所知的小白，到现在leetcode破百的解题数，还是很有成就感的。逻辑思维能力也是明显的有所提高，很多算法当中的思想其实也是可以应用到实际的开发当中的。

因为算法学习总体来说，还是比较枯燥的，就是不断的刷题，前几天，在刷递归回溯算法相关题型的时候，做到了一道解数独的题目，感觉很有意思，花了一点时间做了一个纯前端实现的解数独游戏，在这里分享一下递归回溯法用来解数独的具体实现。

介绍

解数独游戏地址，大家可以点进去试玩一下，就是一个html文件，样式上做的比较简陋，没做兼容性，一般低版本的浏览器可能打开会有问题。想看源码的就直接右键查看源码。

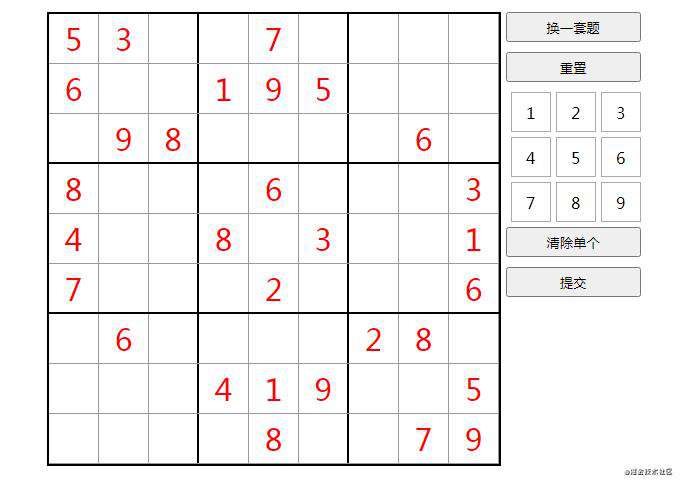
功能很简单，生成一套数独题目，可以手动填入1-9的数据，需要使每一行，每一列，每一个3X3的框中都存在1-9这9个数字。然后可以提交验证看是否答对。

PS：生成一套只有唯一解的数独这块的算法有点难搞，我尝试了很多思路都失败了，所以这里的数独题目目前都是我直接从题库中随机获取的。

解数独

按上图所示的数据，解数独可以抽象成

const board = [
    ["5","3",".",".","7",".",".",".","."],
    ["6",".",".","1","9","5",".",".","."],
    [".","9","8",".",".",".",".","6","."],
    ["8",".",".",".","6",".",".",".","3"],
    ["4",".",".","8",".","3",".",".","1"],
    ["7",".",".",".","2",".",".",".","6"],
    [".","6",".",".",".",".","2","8","."],
    [".",".",".","4","1","9",".",".","5"],
    [".",".",".",".","8",".",".","7","9"]
]

给你一个二维数组，假设给定的数独只有唯一解，你需要编写一个程序，填充空格这些空格，并且需要满足以下三个条件。

• 数字 1-9 在每一行只能出现一次。
• 数字 1-9 在每一列只能出现一次。
• 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

每一个空白格都要选一个数字去填，有多少个空白格，做多少次选择。我们可以想到递归，每次递归填当前的格子。不过我们需要思考一下两个点

1.每次递归的约束条件要怎么去处理？

2.这是个二维数组，怎么使用一个递归方法去处理每一层的数组？

每次递归的约束条件要怎么去处理？

数独的约束条件要求我们每一行，每一列，每一个3X3的宫内，1-9都只能使用一次。

如果按照暴力解法来考虑，每次填入一个值的时候，循环遍历当前节点的行，列，宫，如果不存在重复的值，才能填入值，然后继续递归。

不过我们可以做一些优化，因为每次都循环行列和宫，花费的性能比较大，我们可以定义三个变量用来记录每一行，每一列，每一个宫中使用过的数字，从循环变成查找表的形式，提高性能。

这是个二维数组，怎么使用一个递归方法去处理每一层的数组？

很多递归回溯的题其实只是对于一个一维数组或者字符串的递归，但是这里是二维数组。所以我们需要变通，递归时候定义x,y两个值代表当前节点的x轴和y轴。先从第一行第一位开始递归，x轴不变，每次递归只让y轴加1，当y轴等于9时，说明当前序号为x的数组已经递归完成。我们把x加1，y归0。继续递归下一行的数组。

具体实现

var solveSudoku = function(board) {
  // 定义三个数组来记录，每一行，每一行，每一个3X3里已经被使用过的参数
  let lineX = [];
  let lineY = [];
  let area3x3 = [];
  for (let n = 0; n < 9; n ++) {
    lineX[n] = {};
    lineY[n] = {};
    if (((n + 1) % 3) === 0) {
      const curIndex = (n + 1) / 3;
      area3x3[curIndex - 1] = [{}, {}, {}];
    } 
  }
  // 用来增加（删除）记录，如果已经被使用过，将当前位置置为true
  const toggleCache = (i, j, val, type) => {
    const flag = (type === 'add' ? true : false);
    lineX[i][val] = flag;
    lineY[j][val] = flag;
    area3x3[Math.floor(i / 3)][Math.floor(j / 3)][val] = flag;
  };
  // 判断当前数据是否在当前行，列，3x3中存在
  const hasCache = (i, j, val) => {
    if(lineX[i][val]) return true;
    if(lineY[j][val]) return true;
    if(area3x3[Math.floor(i / 3)][Math.floor(j / 3)][val]) return true;
    return false;
  };
  // 初始化，将初始数据传入记录中
  for (let i = 0; i < 9; i ++) {
    for (let j = 0; j < 9; j ++) {
      const val = board[i][j];
      if (val !== '.') toggleCache(i, j, val, 'add');
    }
  }
  // 递归方法
  const dfs = (xIndex, yIndex) => {
    // 当x轴递归到9时，结束递归。
    // 因为本题都只有唯一解，所以需要return一个true，用来计算出值之后，提前退出
    if (xIndex === 9) return true;
    // 当y轴递归到9时，将x加1，继续下一行的递归
    if (yIndex === 9) return dfs(xIndex + 1, 0);
    if (board[xIndex][yIndex] === '.') {
      // 如果当前没有值，遍历1-9
      for (let v = 1; v <= 9; v ++) {
	// 判断遍历的v是否满足同一行，同一列，3x3都没有被使用过
        if (!hasCache(xIndex, yIndex, String(v))) {
          // 递归
          board[xIndex][yIndex] = String(v);
          toggleCache(xIndex, yIndex, v, 'add');
          // 如果得到的返回值是true，说明已经得到值了，不需要再计算后面的值了，直接退出
          if (dfs(xIndex, yIndex + 1)) return true;
          // 回溯
          board[xIndex][yIndex] = '.';
          toggleCache(xIndex, yIndex, v, 'remove');
        }
      }
    } else {
      // 如果当有初始值，跳到下一个节点
      return dfs(xIndex, yIndex + 1);
    }
  };
  dfs(0, 0);
  return board;
};

总结

没啥说的，就是介绍了递归回溯算法在解数独上的具体实现。

感谢

感谢您的阅读，如果本文对你有帮助，就点个赞支持下吧。